A) 35.60 miles
B) 31.81 miles
C) 26.11 miles
D) 11.27 miles
E) 54.99 miles
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find values for b such that the triangle has one solution. A = 62°, a = 304.6
A)
B)
C)
D)
E)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Use the Law of Sines to solve for C and B.Round your answer to two decimal places. A = 60°, a = 36, c = 40
A) C ≈ 105.79°, B ≈ 45.79°orC ≈ 74.21°, B ≈ 14.21°
B) C ≈ 74.21°, B ≈ 45.79°orC ≈ 105.79°, B ≈ 14.21°
C) C ≈ 10°, B ≈ 110°orC ≈ 25.5°, B ≈ 104.5°
D) C ≈ 45.79°, B ≈ 74.21°orC ≈ 14.21°, B ≈ 105.79°
E) C ≈ 60°, B ≈ 60°orC ≈ 45°, B ≈ 75°
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Write the complex number in trigonometric form. 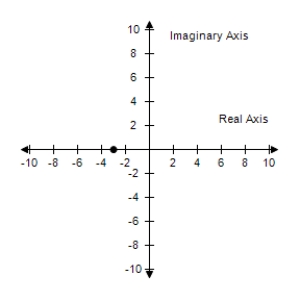
A)
B)
C)
D)
E)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find a unit vector in the direction of the given vector.
A)
B)
C)
D)
E)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Because of prevailing winds, a tree grew so that it was leaning 6° from the vertical.At a point 43 meters from the tree, the angle of elevation to the top of the tree is 30° (see figure) .Find the height a of the tree. 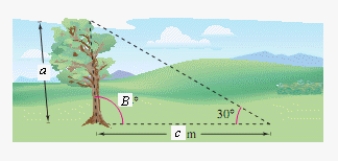 c = 43 m
B = 96°
(Round your answer to two decimal places.)
c = 43 m
B = 96°
(Round your answer to two decimal places.)
A) 24.58 m
B) 26.58 m
C) 25.58 m
D) 28.58 m
E) 27.58 m
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Use the law of Cosines to solve the given triangle.Round your answer to two decimal places.
A = 14, b = 7, C = 118°
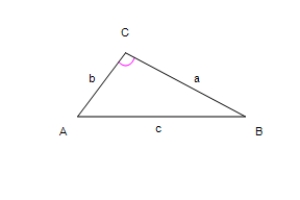
A) A ≈ 42.33°, B ≈ 19.67°, c ≈ 18.36
B) A ≈ 17.67°, B ≈ 17.67°, c ≈ 7
C) A ≈ 44.33°, B ≈ 44.33°, c ≈ 7
D) A ≈ 17.67°, B ≈ 18.36°, c ≈ 18.36
E) A ≈ 44.33°, B ≈ 17.67°, c ≈ 7
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the angle between the vectors. (Round the answer to 2 decimal places.)
A)
B)
C)
D)
E)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Use the vectors , to find the indicated quantity.State whether the result is a vector or a scalar.
A) ; vector
B) -2; scalar
C) 2; scalar
D) ; vector
E) 0; scalar
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Determine whether the Law of Sines or the Law of Cosines is needed to solve the triangle.Then solve the triangle.Round your answer to two decimal places. A = 46°, B = 39°, c = 1.4
A) Law of Cosines; No solution
B) Law of Sines; No solution
C) Law of Cosines; C = 95°, a ≈ 0.88, b ≈ 1.01
D) Law of Sines; C = 95°, a ≈ 1.01, b ≈ 0.88
E) Law of Sines; C = 95°, a ≈ 1.01, b ≈ 1.01
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Represent the following complex number graphically.
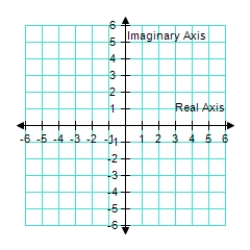
A) ![]()
B) ![]()
C) ![]()
D) ![]()
E) ![]()
Correct Answer

verified
Correct Answer
verified
Multiple Choice
A force of F pounds is required to pull an object weighing W pounds up a ramp inclined at θ degrees from the horizontal. Find F if W = 100 pounds and θ = 11°.Approximate the answer to one decimal place.
A) 18.1 lb
B) 21.1 lb
C) 19.1 lb
D) 20.1 lb
E) 17.1 lb
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Use the Law of Sines to solve (if possible) the triangle.Round your answers to two decimal places. A = 120°, a = b = 36
A) B ≈ 108°, C ≈ 36°, c ≈ 44
B) B ≈ 36°, C ≈ 108°, c ≈ 23.5
C) B ≈ 105°, C ≈ 39°, c ≈ 23.5
D) B ≈ 29°, C ≈ 115°, c ≈ 23.5
E) No Solution
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Given and , find .
A) 0
B) 30
C) 60
D) 61
E) -11
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Using the figure below, sketch a graph of the given vector.[The graphs in the answer choices are drawn to the same scale as the graph below.]
-u ![Using the figure below, sketch a graph of the given vector.[The graphs in the answer choices are drawn to the same scale as the graph below.] -u A) B) C) D) E) none of these](https://d2lvgg3v3hfg70.cloudfront.net/TB7698/11eae838_9cbc_e940_a6c3_c1522820b23e_TB7698_00.jpg)
A) ![]()
B) ![]()
C) ![]()
D) ![]()
E) none of these
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Determine the area of a triangle having the following measurements.Round your answer to two decimal places. B = 64 31 , a = 10 and c = 8.
A) 43.33 sq. units
B) 32.50 sq. units
C) 28.89 sq. units
D) 36.11 sq. units
E) 39.72 sq. units
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the vector v that has a magnitude of 9 and is in the same direction as u, where .
A)
B)
C)
D)
E)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Use the vectors , to find the indicated quantity.State whether the result is a vector or a scalar.
A) ; vector
B) ; vector
C) -72; scalar
D) 60; scalar
E) ; vector
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Determine the angle in the design of the streetlight shown in the following figure.Round your answer upto decimal place. 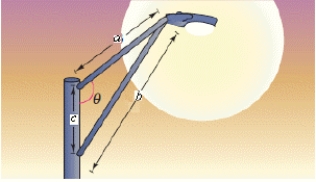
A) 80.5°
B) 95.5°
C) 75.5°
D) 85.5°
E) 90.5°
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Determine whether u are v and orthogonal, parallel, or neither.
A) neither
B) parallel
C) orthogonal
Correct Answer

verified
Correct Answer
verified
Showing 121 - 140 of 304
Related Exams