A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Write the expression as sums or differences of multiples of logarithms. -
A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Determine whether the functions f and g are inverses of each other. -
A) Yes
B)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Determine whether the graph of the function is the graph of a one-to-one function.
-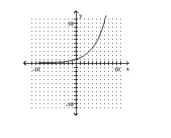
A) Yes
B) No
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Provide an appropriate response. -If and , find .
A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Use the power property to rewrite the expression. -
A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Fill in the blank with one of the words or phrases listed below. Some words or phrases may be used more than once. -The graphs of and are ــــــــــــabout the line .
A) horizontal
B) inverse
C) symmetric
D) vertical
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Use the exponential growth formula to find the final amount. Round to the nearest whole.
-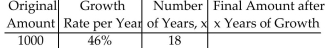
A) 802,831
B)
C)
D) 908,555
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Write the function F(x) as a composition of f, g, or h. -
A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Solve. -Business people are concerned with cost functions, revenue functions, and profit functions. Suppose the revenue for units of a product can be described by , and the cost can be described by . Find the profit for units.
A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Use the exponential decay formula to find the final amount. Round to the nearest whole.
-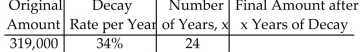
A) 15
B) 10
C) 21
D) 28
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Solve the equation for x. Give an approximate solution accurate to four decimal places. -
A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
If the function is one-to-one, list the inverse function by switching coordinates or inputs and outputs. -f = {(-6, -9) , (6, 9) , (7, 11) , (-7, -11) }
A) f-1 = {(-9, -6) , (9, 6) , (11, 6) , (-11, -7) }
B) f-1 = {(-9, -6) , (-6, 6) , (11, 7) , (-11, -7) }
C) f-1 = {(-9, -6) , (9, 6) , (11, 7) , (-11, -7) }
D) not one-to-one
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Solve for x. -
A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Write the function F(x) as a composition of f, g, or h. -
A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the value of the logarithmic expression. -
A) 5
B) 3
C) 125
D) 25
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Use the exponential decay formula to find the final amount. Round to the nearest whole. -
A) 2594
B) 3330
C) 2964
D) 2941
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Solve the equation. -
A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Graph the exponential function.
-
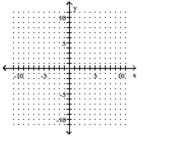
A) ![]()
B) ![]()
C) ![]()
D) ![]()
Correct Answer

verified
Correct Answer
verified
Multiple Choice
For the given functions f and g, find the composition. - Find .
A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Showing 161 - 180 of 300
Related Exams