A) 90°
B) 60°
C) 30°
D) 45°
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Solve the right triangle. -a = 3.6 m, B = 30.3°, C = 90° Round values to one decimal place.
A) A = 59.7°, b = 4.4 m, c = 5.7 m
B) A = 59.7°, b = 2.1 m, c = 4.2 m
C) A = 59.7°, b = 1 m, c = 3.7 m
D) A = 59.7°, b = 4.4 m, c = 4.2 m
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Solve the problem.
-Find a formula for the area of the figure in terms of s. 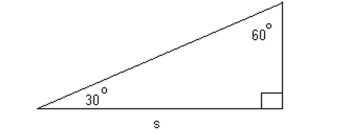
A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Evaluate. -
A) 7
B) 12
C) 84
D) 14
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Solve the problem.
-Find the exact value of x in the figure. 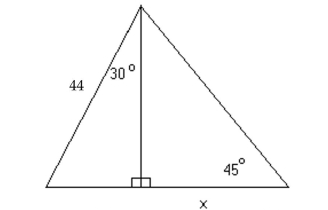
A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find a solution for the equation. Assume that all angles are acute angles. -
A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Solve the problem.
-The index of refraction for air, Ia, is 1.0003. The index of refraction for water, Iw, is 1.3. If , and , find to the nearest tenth.
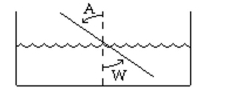
A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Without using a calculator, give the exact trigonometric function value with rational denominator. -sec 45
A)
B) 1
C)
D) °
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Write the function in terms of its cofunction. Assume that any angle in which an unknown appears is an acute angle. -sin 77°
A) csc 13°
B) sin 167°
C) cos 13°
D) cos 77°
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Solve the right triangle. If two sides are given, give angles in degrees and minutes.
-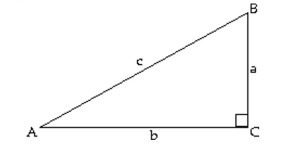 Round the missing side length to two decimal places.
Round the missing side length to two decimal places.
A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Solve the problem for the given information. -Find the equation of a line passing through the origin so that the sine of the angle between the line in quadrant and the positive -axis is .
A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the exact value of the expression. -cos 210°
A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the exact value of the expression. -sec (-1215°)
A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find a value of in [0°, 90°] that satisfies the statement. Leave answer in decimal degrees rounded to seven decimal places, if necessary. -tan ϴ = 1.5047547
A) 56.3935717°
B) 123.606428°
C) 33.6064283°
D) 236.393572°
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find a solution for the equation. Assume that all angles are acute angles. -sec ϴ = csc(ϴ + 46°)
A) 23°
B) 67°
C) 22°
D) 68°
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Suppose ABC is a right triangle with sides of lengths a, b, and c and right angle at C. Find the unknown side length using the Pythagorean theorem and then find the value of the indicated trigonometric function of the given angle. Rationalize the denominator if applicable. -Find when and .
A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Solve the problem. -An airplane travels at 165 km/h for 3 hr in a direction of 174° from a local airport. At the end of this time, how far east of the airport is the plane (to the nearest kilometer) ?
A) 4736 km
B) 492 km
C) 4710 km
D) 52 km
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Use a calculator to find the function value. Give your answer rounded to seven decimal places, if necessary. -cos 47° cos 133° - sin 47° sin 133°
A) 2
B) 0
C) 1
D) -1
Correct Answer

verified
Correct Answer
verified
True/False
Use a calculator to decide whether the statement is true or false. -cos (2 ·30°)= 2 · cos 30°
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Solve the problem. -The grade resistance F of a car traveling up or down a hill is modeled by the equation F = W sin ϴ, where W is the weight of the car and ϴ is the angle of the hill's grade (ϴ > 0 for uphill travel, ϴ < 0 For downhill travel) . What is the grade resistance (to the nearest pound) of a 2100-lb car traveling Downhill on a 5° grade (ϴ = -5°) ?
A) 183 lb
B) -2105 lb
C) 2105 lb
D) -183 lb
Correct Answer

verified
Correct Answer
verified
Showing 121 - 140 of 204
Related Exams