Filters
Question type
Study Flashcards

Determine whether the given functions are inverses of each other. - f(x) =x,x≥0,g(x) =x2,x≥0f ( x ) = \sqrt { x } , x \geq 0 , \quad g ( x ) = x ^ { 2 } , x \geq 0


A) Yes
B) No

Correct Answer

verifed

verified

A

Solve the equation. - ln⁡x+ln⁡(x−1) =ln⁡2\ln x + \ln ( x - 1 ) = \ln 2


A) 2, -1
B) -1
C) 32\frac { 3 } { 2 }
D) 2

Correct Answer

verifed

verified

Evaluate. - 7log⁡101.67 \log 10 ^ { 1.6 }


A) 11.2
B) 1.12
C) 3.2900
D) 112

Correct Answer

verifed

verified

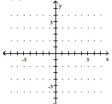
Graph the function. - f(x) =3−xf ( x ) = 3 ^ { - x } Graph the function. - f ( x ) = 3 ^ { - x } A) B) C) D)


A) Graph the function. - f ( x ) = 3 ^ { - x } A) B) C) D)
B) Graph the function. - f ( x ) = 3 ^ { - x } A) B) C) D)
C) Graph the function. - f ( x ) = 3 ^ { - x } A) B) C) D)
D) Graph the function. - f ( x ) = 3 ^ { - x } A) B) C) D)

Correct Answer

verifed

verified

A one-to-one function f is given.  Find f−1(x) \text { Find } \mathrm { f } ^ { - 1 } ( \mathrm { x } ) and graph fwith a solid line and f−1(x) f ^ { - 1 } ( x ) with a dotted line on the same axes. - f(x) =x3+1f ( x ) = x ^ { 3 } + 1 A one-to-one function f is given. \text { Find } \mathrm { f } ^ { - 1 } ( \mathrm { x } ) and graph fwith a solid line and f ^ { - 1 } ( x ) with a dotted line on the same axes. - f ( x ) = x ^ { 3 } + 1 A) f ^ { - 1 } ( x ) = - \sqrt [ 3 ] { x - 1 } B) f ^ { - 1 } ( x ) = \sqrt [ 3 ] { x - 1 } C) f ^ { - 1 } ( x ) = - x ^ { 3 } + 1 D) f ^ { - 1 } ( x ) = - x ^ { 3 } - 1


A) f−1(x) =−x−13f ^ { - 1 } ( x ) = - \sqrt [ 3 ] { x - 1 }
A one-to-one function f is given. \text { Find } \mathrm { f } ^ { - 1 } ( \mathrm { x } ) and graph fwith a solid line and f ^ { - 1 } ( x ) with a dotted line on the same axes. - f ( x ) = x ^ { 3 } + 1 A) f ^ { - 1 } ( x ) = - \sqrt [ 3 ] { x - 1 } B) f ^ { - 1 } ( x ) = \sqrt [ 3 ] { x - 1 } C) f ^ { - 1 } ( x ) = - x ^ { 3 } + 1 D) f ^ { - 1 } ( x ) = - x ^ { 3 } - 1
B) f−1(x) =x−13f ^ { - 1 } ( x ) = \sqrt [ 3 ] { x - 1 }
A one-to-one function f is given. \text { Find } \mathrm { f } ^ { - 1 } ( \mathrm { x } ) and graph fwith a solid line and f ^ { - 1 } ( x ) with a dotted line on the same axes. - f ( x ) = x ^ { 3 } + 1 A) f ^ { - 1 } ( x ) = - \sqrt [ 3 ] { x - 1 } B) f ^ { - 1 } ( x ) = \sqrt [ 3 ] { x - 1 } C) f ^ { - 1 } ( x ) = - x ^ { 3 } + 1 D) f ^ { - 1 } ( x ) = - x ^ { 3 } - 1
C) f−1(x) =−x3+1f ^ { - 1 } ( x ) = - x ^ { 3 } + 1
A one-to-one function f is given. \text { Find } \mathrm { f } ^ { - 1 } ( \mathrm { x } ) and graph fwith a solid line and f ^ { - 1 } ( x ) with a dotted line on the same axes. - f ( x ) = x ^ { 3 } + 1 A) f ^ { - 1 } ( x ) = - \sqrt [ 3 ] { x - 1 } B) f ^ { - 1 } ( x ) = \sqrt [ 3 ] { x - 1 } C) f ^ { - 1 } ( x ) = - x ^ { 3 } + 1 D) f ^ { - 1 } ( x ) = - x ^ { 3 } - 1
D) f−1(x) =−x3−1f ^ { - 1 } ( x ) = - x ^ { 3 } - 1
A one-to-one function f is given. \text { Find } \mathrm { f } ^ { - 1 } ( \mathrm { x } ) and graph fwith a solid line and f ^ { - 1 } ( x ) with a dotted line on the same axes. - f ( x ) = x ^ { 3 } + 1 A) f ^ { - 1 } ( x ) = - \sqrt [ 3 ] { x - 1 } B) f ^ { - 1 } ( x ) = \sqrt [ 3 ] { x - 1 } C) f ^ { - 1 } ( x ) = - x ^ { 3 } + 1 D) f ^ { - 1 } ( x ) = - x ^ { 3 } - 1

Correct Answer

verifed

verified

Solve the equation without using a calculator. - 3x=193 ^ { x } = \frac { 1 } { 9 }


A) 2
B) -2
C) 13
D) 12

Correct Answer

verifed

verified

B

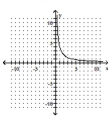
A one-to-one function f is given.  Find f−1(x) \text { Find } \mathrm { f } ^ { - 1 } ( \mathrm { x } ) and graph fwith a solid line and f−1(x) f ^ { - 1 } ( x ) with a dotted line on the same axes. - f(x) =4x,x≥0f ( x ) = \frac { 4 } { x } , x \geq 0 A one-to-one function f is given. \text { Find } \mathrm { f } ^ { - 1 } ( \mathrm { x } ) and graph fwith a solid line and f ^ { - 1 } ( x ) with a dotted line on the same axes. - f ( x ) = \frac { 4 } { x } , x \geq 0 A) \mathrm { f } ^ { - 1 } ( \mathrm { x } ) = \frac { 4 } { \mathrm { x } } , \mathrm { x } \leq 0 B) f ^ { - 1 } ( x ) = \frac { 4 } { x } , x \geq 0 ; f ( x ) = f ^ { - 1 } ( x ) C) \mathrm { f } ^ { - 1 } ( \mathrm { x } ) = - \frac { 4 } { \mathrm { x } } , \mathrm { x } \geq 0 D) f ^ { - 1 } ( x ) = - \frac { 4 } { x } , x \leq 0


A) f−1(x) =4x,x≤0\mathrm { f } ^ { - 1 } ( \mathrm { x } ) = \frac { 4 } { \mathrm { x } } , \mathrm { x } \leq 0
A one-to-one function f is given. \text { Find } \mathrm { f } ^ { - 1 } ( \mathrm { x } ) and graph fwith a solid line and f ^ { - 1 } ( x ) with a dotted line on the same axes. - f ( x ) = \frac { 4 } { x } , x \geq 0 A) \mathrm { f } ^ { - 1 } ( \mathrm { x } ) = \frac { 4 } { \mathrm { x } } , \mathrm { x } \leq 0 B) f ^ { - 1 } ( x ) = \frac { 4 } { x } , x \geq 0 ; f ( x ) = f ^ { - 1 } ( x ) C) \mathrm { f } ^ { - 1 } ( \mathrm { x } ) = - \frac { 4 } { \mathrm { x } } , \mathrm { x } \geq 0 D) f ^ { - 1 } ( x ) = - \frac { 4 } { x } , x \leq 0
B) f−1(x) =4x,x≥0;f(x) =f−1(x) f ^ { - 1 } ( x ) = \frac { 4 } { x } , x \geq 0 ; f ( x ) = f ^ { - 1 } ( x )
A one-to-one function f is given. \text { Find } \mathrm { f } ^ { - 1 } ( \mathrm { x } ) and graph fwith a solid line and f ^ { - 1 } ( x ) with a dotted line on the same axes. - f ( x ) = \frac { 4 } { x } , x \geq 0 A) \mathrm { f } ^ { - 1 } ( \mathrm { x } ) = \frac { 4 } { \mathrm { x } } , \mathrm { x } \leq 0 B) f ^ { - 1 } ( x ) = \frac { 4 } { x } , x \geq 0 ; f ( x ) = f ^ { - 1 } ( x ) C) \mathrm { f } ^ { - 1 } ( \mathrm { x } ) = - \frac { 4 } { \mathrm { x } } , \mathrm { x } \geq 0 D) f ^ { - 1 } ( x ) = - \frac { 4 } { x } , x \leq 0
C) f−1(x) =−4x,x≥0\mathrm { f } ^ { - 1 } ( \mathrm { x } ) = - \frac { 4 } { \mathrm { x } } , \mathrm { x } \geq 0
A one-to-one function f is given. \text { Find } \mathrm { f } ^ { - 1 } ( \mathrm { x } ) and graph fwith a solid line and f ^ { - 1 } ( x ) with a dotted line on the same axes. - f ( x ) = \frac { 4 } { x } , x \geq 0 A) \mathrm { f } ^ { - 1 } ( \mathrm { x } ) = \frac { 4 } { \mathrm { x } } , \mathrm { x } \leq 0 B) f ^ { - 1 } ( x ) = \frac { 4 } { x } , x \geq 0 ; f ( x ) = f ^ { - 1 } ( x ) C) \mathrm { f } ^ { - 1 } ( \mathrm { x } ) = - \frac { 4 } { \mathrm { x } } , \mathrm { x } \geq 0 D) f ^ { - 1 } ( x ) = - \frac { 4 } { x } , x \leq 0
D) f−1(x) =−4x,x≤0f ^ { - 1 } ( x ) = - \frac { 4 } { x } , x \leq 0
A one-to-one function f is given. \text { Find } \mathrm { f } ^ { - 1 } ( \mathrm { x } ) and graph fwith a solid line and f ^ { - 1 } ( x ) with a dotted line on the same axes. - f ( x ) = \frac { 4 } { x } , x \geq 0 A) \mathrm { f } ^ { - 1 } ( \mathrm { x } ) = \frac { 4 } { \mathrm { x } } , \mathrm { x } \leq 0 B) f ^ { - 1 } ( x ) = \frac { 4 } { x } , x \geq 0 ; f ( x ) = f ^ { - 1 } ( x ) C) \mathrm { f } ^ { - 1 } ( \mathrm { x } ) = - \frac { 4 } { \mathrm { x } } , \mathrm { x } \geq 0 D) f ^ { - 1 } ( x ) = - \frac { 4 } { x } , x \leq 0

Correct Answer

verifed

verified

Evaluate. - log⁡71343\log _ { 7 } \frac { 1 } { 343 }


A) -3
B) 49
C) -49
D) 3

Correct Answer

verifed

verified

Solve the equation. - ln⁡x=32ln⁡64\ln x = \frac { 3 } { 2 } \ln 64


A) 96
B) 512
C) 1283\frac { 128 } { 3 }
D) 2.7093

Correct Answer

verifed

verified

Solve the equation. - ln⁡(14) −ln⁡x=ln⁡(x−5) \ln ( 14 ) - \ln x = \ln ( x - 5 )


A) 7
B) 192\frac { 19 } { 2 }
C) 7, -2
D) -2

Correct Answer

verifed

verified

Find the value obtained when 10 is raised to the given exponent. Round to three significant digits. --1.4375


A) 27.4
B) -0.0365
C) 0.0365
D) -27.4

Correct Answer

verifed

verified

Determine whether the function is a one-to-one function. - y=(x+5) 3y = ( x + 5 ) ^ { 3 }


A) Yes
B) No

Correct Answer

verifed

verified

Solve the equation without using a calculator. - 3−x=193 ^ { - x } = \frac { 1 } { 9 }


A) 2
B) 13\frac { 1 } { 3 }
C) 12\frac { 1 } { 2 }
D) -2

Correct Answer

verifed

verified

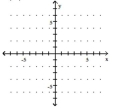
Graph the function. - f(x) =2x+1f ( x ) = 2 ^ { x } + 1 Graph the function. - f ( x ) = 2 ^ { x } + 1 A) B) C) D)


A) Graph the function. - f ( x ) = 2 ^ { x } + 1 A) B) C) D)
B) Graph the function. - f ( x ) = 2 ^ { x } + 1 A) B) C) D)
C) Graph the function. - f ( x ) = 2 ^ { x } + 1 A) B) C) D)
D) Graph the function. - f ( x ) = 2 ^ { x } + 1 A) B) C) D)

Correct Answer

verifed

verified

Find the antilog of the logarithm. Round the answer to six decimal places. --1.4972


A) 4.469158
B) 31.419553
C) 0.708402
D) 0.031827

Correct Answer

verifed

verified

Use properties of logarithms to expand the logarithmic expression as much as possible. - log⁡ey−z\log _ { e } y ^ { - z }


A) −zlog⁡ey- z \log _ { \mathrm { e } } \mathrm { y }
B) −ylog⁡ez- y \log _ { e } z
C) ylog⁡ezy \log _ { e } z
D) zlog⁡eyz \log _ { e } y

Correct Answer

verifed

verified

Determine whether the given function is one-to-one. If it is one-to-one, find its inverse function. - f(x) =x2−1,x≥0f ( x ) = x ^ { 2 } - 1 , x \geq 0


A) f−1(x) =x+1,x≥0f ^ { - 1 } ( x ) = \sqrt { x } + 1 , x \geq 0
B) f−1(x) =x+1,x≥−1\mathrm { f } ^ { - 1 } ( \mathrm { x } ) = \sqrt { \mathrm { x } + 1 } , \mathrm { x } \geq - 1
C) f−1(x) =x−1,x≥1f ^ { - 1 } ( x ) = \sqrt { x - 1 } , x \geq 1
D) not a one-to-one function

Correct Answer

verifed

verified

Determine whether the function is a one-to-one function. -Determine whether the function is a one-to-one function. - A) Yes B) No


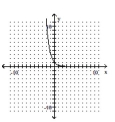
A) Yes
B) No

Correct Answer

verifed

verified

A

For the given functions f and g , find the indicated composition. - f(x) =x−710,g(x) =10x+7(g∘f) (x) \begin{array} { l } f ( x ) = \frac { x - 7 } { 10 } , \quad g ( x ) = 10 x + 7 \\( g \circ f ) ( x ) \end{array}


A) x−710x - \frac { 7 } { 10 }
B) 10x + 63
C) x
D) x + 14

Correct Answer

verifed

verified

Solve for the indicated variable. - P=110e6t, for tP = 110 e ^ { 6 t } , \text { for } t


A) t=ln⁡P+ln⁡1106\mathrm { t } = \frac { \ln \mathrm { P } + \ln 110 } { 6 }
B) t=ln⁡(P−110) 6t = \frac { \ln ( P - 110 ) } { 6 }
C) t=P110e6t = \frac { P } { 110 e ^ { 6 } }
D) t=ln⁡P−ln⁡1106t = \frac { \ln P - \ln 110 } { 6 }

Correct Answer

verifed

verified

Showing 1 - 20 of 229

Related Exams

Exam 1

Basic Concepts

306 Questions

Exam 2

Equations and Inequalities

234 Questions

Exam 3

Graphs and Functions

61 Questions

Exam 4

Systems of Equations and Inequalities

116 Questions

Exam 5

Polynomials and Polynomial Functions

112 Questions

Exam 6

Rational Expressions and Equations

130 Questions

Exam 7

Roots, Radicals, and Complex Numbers

298 Questions

Exam 8

Quadratic Functions

221 Questions

Exam 10

Characteristics of Functions and Their Graphs

142 Questions

Exam 11

Conic Sections

132 Questions

Exam 12

Sequences, Series, and Probability

208 Questions

Show Answer