A) having it edited and typeset and selling 2,800 copies.
B) not having it edited and typeset and not selling any copies.
C) having it edited and typeset and selling 5,600 copies.
D) having it edited and typeset and selling 3,000 copies.
E) having it typeset and selling 1,400 copies.
Correct Answer

verified
Correct Answer
verified
Multiple Choice
A profit-maximizing monopoly faces an inverse demand function described by the equation p(y) = 50 - y and its total costs are c(y) = 10y, where prices and costs are measured in dollars. In the past it was not taxed, but now it must pay a tax of 2 dollars per unit of output. After the tax, the monopoly will
A) leave its price constant.
B) increase its price by 2 dollars.
C) increase its price by 3 dollars.
D) increase its price by 1 dollar.
E) None of the above.
Correct Answer

verified
Correct Answer
verified
Multiple Choice
In Problem 1, if the demand schedule for Bong's book is Q = 5,000 - 100p, the cost of having the book typeset is $6,000, and the marginal cost of printing an extra book is $4, then he would maximize his profits by
A) not having it typeset and not selling any copies.
B) having it typeset and selling 4,600 copies.
C) having it typeset and selling 2,500 copies.
D) having it typeset and selling 2,300 copies.
E) having it typeset and selling 1,150 copies.
Correct Answer

verified
Correct Answer
verified
Multiple Choice
In Problem 1, if the demand schedule for Bong's book is Q = 2,000 - 100p, the cost of having the book typeset is $9,000, and the marginal cost of printing an extra book is $4, then he would maximize his profits by
A) having it typeset and selling 1,600 copies.
B) not having it typeset and not selling any copies.
C) having it typeset and selling 1,000 copies.
D) having it typeset and selling 800 copies.
E) having it typeset and selling 400 copies.
Correct Answer

verified
Correct Answer
verified
Multiple Choice
In Problem 2, if the demand for pigeon pies is given by p(y) = 140 - 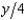 , then the level of output that will maximize Peter's profit is
, then the level of output that will maximize Peter's profit is
A) 56.
B) 560.
C) 284.
D) 840.
E) None of the above.
Correct Answer

verified
Correct Answer
verified
Multiple Choice
In Problem 1, if the demand schedule for Bong's book is Q = 3,000 - 100p, the cost of having the book typeset is $10,000, and the marginal cost of printing an extra book is $4, then he would maximize his profits by
A) having it typeset and selling 1,300 copies.
B) having it typeset and selling 1,500 copies.
C) having it typeset and selling 2,600 copies.
D) not having it typeset and not selling any copies.
E) having it typeset and selling 650 copies.
Correct Answer

verified
Correct Answer
verified
Multiple Choice
A firm has invented a new beverage called Slops. It doesn't taste very good, but it gives people a craving for Lawrence Welk's music and Professor Johnson's jokes. Some people are willing to pay money for this effect, so the demand for Slops is given by the equation q = 20 - p. Slops can be made at zero marginal cost from old-fashioned macroeconomics books dissolved in bathwater. But before any Slops can be produced, the firm must undertake a fixed cost of $105. Since the inventor has a patent on Slops, it can be a monopolist in this new industry.
A) The firm will produce 10 units of Slops.
B) From the point of view of social efficiency, it is best that no Slops be produced.
C) A Pareto improvement could be achieved by having the government pay the firm a subsidy of $110 and insisting that the firm offer Slops at zero price.
D) The firm will produce 20 units of Slops.
E) None of the above.
Correct Answer

verified
Correct Answer
verified
Multiple Choice
In Problem 2, if the demand for pigeon pies is given by p(y) = 110 - 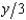 , then the level of output that will maximize Peter's profit is
, then the level of output that will maximize Peter's profit is
A) 169.
B) 33.
C) 330.
D) 495.
E) None of the above.
Correct Answer

verified
Correct Answer
verified
Multiple Choice
A profit-maximizing monopoly faces an inverse demand function described by the equation p(y) = 30 - y and its total costs are c(y) = 6y, where prices and costs are measured in dollars. In the past it was not taxed, but now it must pay a tax of 2 dollars per unit of output. After the tax, the monopoly will
A) increase its price by 2 dollars.
B) increase its price by 3 dollars.
C) increase its price by 1 dollar.
D) leave its price constant.
E) None of the above.
Correct Answer

verified
Correct Answer
verified
Multiple Choice
In Problem 2, if the demand for pigeon pies is given by p(y) = 140 -  , then the level of output that will maximize Peter's profit is
, then the level of output that will maximize Peter's profit is
A) 28.
B) 420.
C) 280.
D) 140.
E) None of the above.
Correct Answer

verified
Correct Answer
verified
Showing 21 - 30 of 30
Related Exams